Die Netzimpedanz ist ein entscheidender Faktor für das Verhalten und die Stabilität von Stromnetzen. Sie beschreibt das Zusammenspiel von Spannung und Strom und beeinflusst maßgeblich, wie elektrische Energie durch das Netz fließt. Eine genaue Kenntnis der Netzimpedanz ist unerlässlich, da Abweichungen nicht nur die Qualität der Stromversorgung beeinträchtigen, sondern auch Resonanzen im Netz verursachen können. Diese Resonanzen können zu erheblichen Problemen führen, indem sie unerwünschte Schwingungen verstärken und so das Netz sowie angeschlossene Geräte schädigen. In diesem Beitrag werden die Grundlagen der Netzimpedanz sowie deren Auswirkungen auf Resonanzen und die Netzstabilität näher erläutert.
Was ist Power Quality und wie wird sie gemessen?
Die Eigenschaften eines elektrischen Energieversorgungsnetzes werden anhand einer Vielzahl von Parametern beschrieben. Die Berechnung dieser Parameter, etwa der Netzfrequenz oder des Spannungsverzerrungsfaktors THD, ist in verschiedenen Normen und Richtlinien definiert. Diese enthalten ebenfalls Vorgaben und Grenzwerte, die während des Betriebs eingehalten werden müssen, um eine zuverlässige und störungsfreie Stromversorgung zu gewährleisten.
Für die Nutzung elektrischer Energie in Wechselstromnetzen ist eine konstante Netzfrequenz, eine gleichbleibende Versorgungsspannung und eine perfekte Sinus-Kurvenform der Versorgungsspannung wünschenswert. Durch die räumliche Ausdehnung und die Vielzahl an unterschiedlichen Verbrauchern und Erzeugern ergeben sich in der Praxis jedoch Abweichungen. Das Beziehen von elektrischer Energie verursacht Ströme, die wiederum zu Spannungsfällen über die Leitungen und Komponenten des Netzes führen. Die Höhe der Versorgungsspannung für einen Netznutzer ist entsprechend abhängig vom Zusammenwirken aller Spannungsfälle im Netzbereich, das den Nutzer versorgt. Ein weiteres Beispiel ist die Variation der Netzfrequenz. Zum Erhalt einer konstanten Netzfrequenz muss in jedem Augenblick ein perfektes Gleichgewicht zwischen Erzeugerleistung und Verbraucherleistung herrschen, also die gleiche Menge Energie ins Netz eingespeist werden, wie aktuell nachgefragt wird. Ein Ungleichgewicht führt entsprechend zu einem Abfall oder Anstieg der Netzfrequenz. Es gibt also ein Zusammenspiel zwischen Erzeugung und Verbrauch der elektrischen Energie, dass die verschiedenen Parameter beeinflusst. Generell lässt sich festhalten, dass jeder elektrische Verbraucher während seines Betriebs als auch beim Ein- und Ausschalten Netzrückwirkungen erzeugt. Die Vielzahl an angeschlossenen Verbrauchern beeinflusst das Netz somit durch Störaussendungen und nichtlineare Strom-Spannungs-Kennlinien, wie sie vermehrt bei leistungselektronischen Geräten vorkommen.
Unter dem Begriff Power Quality wird die Übereinstimmung zwischen den geforderten Eigenschaften der Netzspannung und des Stromes und den Eigenschaften der gelieferten Elektrizität verstanden. Bewegen sich die Parameter innerhalb der in den gültigen Normen und Richtlinien definierten Grenzen, können angeschlossene Geräte einwandfrei betrieben werden und es ist davon auszugehen, dass diese keine Schäden nehmen.
Die Begriffe Power Quality und Spannungsqualität werden häufig austauschbar eingesetzt, da die Spannung die Power Quality beim Netznutzer maßgeblich beeinflusst. Der Begriff Power Quality beinhaltet jedoch sowohl Spannungs- als auch Stromqualität. Zu den Bewertungskriterien für Power Quality zählen:
- Netzfrequenz
- Langsame Spannungsänderungen/Spannungshöhe
- Schnelle Spannungsänderungen
- Flicker
- Spannungseinbrüche
- Kurze/lange Unterbrechungen
- Transiente
- Unsymmetrien
- Oberschwingungen
Die Messung von Power Quality gewinnt mit der fortschreitenden Integration erneuerbarer Energien und der vermehrten Verwendung leistungselektronischer Geräte immer mehr an Wichtigkeit. Es lassen sich zwei Arten der Messung von Power Quality unterscheiden: kurzzeitige Netzanalysen und langfristiges, dauerhaftes Monitoring.
Bei kurzzeitigen Netzanalysen wird die Power Quality an einem Ort bestimmt, um den aktuellen Zustand des Netzes zu erfassen. Soll an dieser Stelle beispielsweise eine Produktionsanlage aufgebaut werden, so kann mit dem gewonnenen Wissen eine Aussage getroffen werden, ob der Standort geeignet ist. Auch bei wiederkehrenden Problemen oder Ausfällen von Produktionsanlagen kann die Bestimmung von Power Quality helfen, um geeignete Maßnahmen zu entwickeln, die zu einer Verbesserung der Power Quality führen. Beim dauerhaften Monitoring wird der Power Quality im Netz dauerhaft überwacht, um langfristige Trends frühzeitig zu erfassen und rechtzeitig geeignete Gegenmaßnahmen zu ergreifen, sollte es zu schädlichen Veränderungen kommen.
Was sind Oberschwingungen?
Die Frequenzanteile in der Netzspannung oder im Strom, die von der Netznennfrequenz, im europäischen Verbundnetz 50Hz, abweichen, werden als Oberschwingungen bezeichnet. Entsprechen sie dabei einem ganzzahligen Vielfachen der Grundfrequenz, also etwa 100Hz oder 150Hz, dann werden diese auch Harmonische genannt. So ist etwa 150Hz die 3. Harmonische, da es sich um die dreifache Grundfrequenz handelt. Die Netzspannung, die der Netznutzer erhält, setzt sich aus der Überlagerung der Grundfrequenz mit allen Oberschwingungsanteilen zusammen. Die Oberschwingungen sind entsprechend unerwünschte Frequenzen, die die Qualität der Netzspannung verschlechtern, da diese idealerweise durch eine perfekte Sinuskurve dargestellt wird.
Oberschwingungen und Harmonische entstehen durch nicht-lineare Betriebsmittel. Das heißt, dass der von einer nicht-linearen Last entnommene Strom oder von einem solchen Erzeuger eingespeiste Strom nicht sinusförmig ist oder etwa periodisch ein- und ausgeschaltet wird. Die Ströme verursachen entsprechende Spannungsabfälle verschiedener Frequenzen, die dann die Netzspannung verzerren. Nicht-lineare Lasten sind etwa Energiesparlampen, Wechselrichter und Schaltnetzteile.
Für Betriebsmittel und ans Netz angeschlossene Geräte sind Oberschwingungen schlecht und können zu Fehlfunktionen, Überlastung, Alterung, Leistungseinbußen oder zur Beschädigung und Zerstörung führen. Ein Problem sind Oberschwingungen auch für Kabel, da diese für die durch sie fließenden Ströme ausgelegt sein müssen. Betrachtet man beispielsweise ein symmetrisch belastetes Drehstromnetz, dann zeigt sich, dass die Grundschwingungen im Neutralleiter sich durch Überlagerung aufheben, die Oberschwingungen jedoch addieren. Diese zusätzliche Belastung muss bei der Auslegung der Kabel entsprechend berücksichtigt werden.
Zur Vermeidung und Verminderung von Oberschwingungen können beispielsweise Filter (Saugkreise) genutzt werden. Diese Filter besitzen für die entsprechenden Frequenzen eine sehr niedrige Impedanz und leiten die entsprechenden Anteile dann ab.
Was ist Power Quality Monitoring?
Unter Power Quality Monitoring wird die kontinuierliche Überwachung des Netzes oder einer Anlage im Hinblick auf Power Quality Parameter verstanden. Durch die kontinuierliche Messung lassen sich Tendenzen und Probleme frühzeitig erkennen, sodass rechtzeitig Maßnahmen entwickelt werden können, die weitergehende Schäden und Störungen vermeiden.
Auch bei Fehlerfällen und unvorhergesehenen Ausfällen erlauben die durch die kontinuierliche Überwachung aufgenommenen Daten Rückschlüsse auf die Ursache. Mit ihnen können Abhilfemaßnahmen entwickelt werden, sodass das Problem künftig nicht mehr auftritt und nachhaltig gelöst werden kann. Eine weitere sinnvolle Anwendung ist die Nutzung von Power Quality Daten zur Netzplanung. Sie können genutzt werden, um zu erkennen, an welchen Stellen ein vorhandenes Netz noch freie Kapazitäten aufweist oder gegebenenfalls bereits am Leistungsmaximum genutzt wird. Power Quality Monitoring kann jedoch auch helfen Energie zu sparen, da unerwünschte Leistungsflüsse im Netz erkannt werden können.
Was sind Impedanzen und was ist die Netzimpedanz?
Das Verhalten elektrischer Bauteile und Schaltungen ist grundsätzlich von der Frequenz f der Betriebsspannung und des Stromes abhängig. Analog zu Gleichstromkreisen, in denen das Verhältnis von Spannung U und Strom I über den Widerstandswert R gekennzeichnet wird, beschreibt die Impedanz das Verhältnis von Spannung U und Strom I bei einer beliebigen Frequenz. Die Impedanz kennzeichnet somit den frequenzabhängigen Widerstand elektrischer Komponenten, wie einer Spule, einem Kondensator oder einem Widerstand. Sie ist damit eine wichtige Größe der komplexen Wechselstromtechnik und wird mit dem Formelzeichen Z gekennzeichnet.
Als komplexe Größe setzt sich die Impedanz aus einem Realteil R und einem Imaginärteil X zusammen und kann als Zeiger in der gauss’schen Zahlenebene dargestellt werden. Der Imaginärteil X wird auch als Reaktanz bezeichnet. Alternativ zur Darstellung über Real- und Imaginärteil kann die Impedanz über den Betrag |Z| und die Phase ϕ charakterisiert werden.
Häufig wird der Kehrwert der Impedanz verwendet, der als Admittanz Y bezeichnet wird und folgendermaßen mit der Impedanz zusammenhängt:
$$Y = \frac{1}{Z}$$
Die Impedanz ZL einer idealen Spule mit der Induktivität L steigt linear mit der Frequenz f an und ist rein imaginär. Sie wird nach folgender Gleichung berechnet
$$Z_L = j 2 \pi f L$$
und ist in Abbildung 1 dargestellt. Für den Plot wurde eine Induktivität von 1mH gewählt.
Im Gegensatz zur Impedanz einer Spule verhält sich die Impedanz ZC eines idealen Kondensators mit der Kapazität C umgekehrt proportional zur Frequenz f und ergibt sich nach folgender Formel:
$$Z_C = \frac{1}{j 2 \pi f C}$$
Abbildung 2 zeigt den Betragsverlauf der Impedanz für eine Kapazität von 1µF.
Die gewählten Werte von L = 1mH und C = 1µF entsprechen typischen Werten einer Freileitung mit 1 km Länge.
Das elektrische Energieversorgungssystem besteht aus einer Vielzahl an Einspeiseanlagen, Leitungen und Verbrauchern. Alle diese Betriebsmittel weisen frequenzabhängige Kapazitäts-, Induktivitäts- und Widerstandsbeläge und somit ein frequenzabhängiges Verhalten auf. Die spektrale Netzimpedanz bezeichnet den frequenzabhängigen Widerstand, der von jedem beliebigen Netzverknüpfungspunkt gemessen werden kann. Sie bildet die Summe aller Impedanzen, die hinter dem Messpunkt auftreten. Da sich die Topologie und der Zustand des Energieversorgungssystems durch Schalthandlungen ständig ändern, ist die Netzimpedanz im Allgemeinen zeitabhängig.
Die Netzimpedanz ZN ist eine wichtige Größe zur Berechnung der transienten Kurzschlussleistung, die an einem Netzverknüpfungspunkt zur Verfügung steht. Die transiente Kurzschlussleistung SK wird typischerweise über folgende Formel abgeschätzt:
$$ S_K = 1.1 \frac{(U_N)^2}{Z_{N}} $$
Dabei bezeichnet UN die Nennspannung des Netzes. Mit der Kurzschlussleistung kann die Beanspruchung des Netzes am Verküpfungspunkt im Kurzschlussfall quantifiziert und insbesondere Leistungsschalter dimensioniert werden. Die Kurzschlussleistung ist allerdings keine physikalische Größe sondern nur eine Bemessungsgröße, da im Kurzschlussfall die Spannung auf 0V abfällt, für die Berechnung der Kurzschlussleistung aber die Nennspannung verwendet wird. Mit der Kurzschlussleistung kann weiterhin eine Aussage darüber getroffen werden, wie stark die Spannung im Kurzschlussfall an umliegenden Netzknoten absinkt. Das Phänomen wird als Spannungstrichter bezeichnet. Liegt im Netz ein hoher Vermaschungsgrad vor, so ist die Netzimpedanz klein und es ergibt sich eine große Kurzschlussleistung. Folglich ergibt sich ein schmaler Spannungstrichter im Kurzschlussfall.
Was sind Netzresonanzen und warum können sie gefährlich sein?
Jedes schwingfähige System weist Eigenschwingungen auf. Werden die Eigenschwingungen angeregt, so beginnt das System bei diesen Frequenzen zu schwingen. Das Phänomen wird als Resonanz bezeichnet. Ein anschauliches Beispiel aus der Akustik ist eine Stimmgabel.

Die Eigenfrequenz einer typischen Stimmgabel liegt bei 440Hz und kann beispielsweise über einen Anschläger angeregt werden. Der Holzkörper unterhalb der Stimmgabel wird als Resonanzkörper bezeichnet. Beginnt die Stimmgabel mit ihrer Eigenfrequenz zu schwingen, so beginnt der Resonanzkörper ebenfalls zu schwingen und verstärkt den Ton. Wird die Stimmgabel nur einmalig angeschlagen, so verklingt der Ton nach kurzer Zeit. Die akustische Schwingung wird gedämpft.
Wird ein System periodisch mit seiner Eigenfrequenz angeregt und ist nur schwach gedämpft, so kann die Amplitude der Schwingung immer weiter ansteigen, bis es zu einer Resonanzkatastrophe kommt. Das schwingende System kann in diesem Fall der Schwingungsamplitude nicht mehr standhalten und wird zerstört. Ein populäres Beispiel bietet die Tacoma-Narrows-Brücke, die im Jahr 1940 aufgrund einer Resonanzkatastrophe einstürzte und in Abbildung 3 zu sehen ist. Zuvor hatten periodische Windböen die Brücke zu starken Schwingungen angeregt.

Resonanzen können in jedem beliebigen Schaltkreis mit reaktiven Elementen auftreten. Ein simples schwingfähiges System wird durch eine Kapazität und eine Induktivität gebildet. Energie wird beim Aufladen des (idealen) Kondensators im elektrischen Feld gespeichert und beim Entladen über die (ideale) Spule in magnetische Energie umgesetzt. Dieser Vorgang wiederholt sich periodisch. Im Resonanzfall wird das System mit einer Frequenz nahe seiner Eigenfrequenz angeregt. Die einfachsten realen elektrischen Schwingkreise stellen ein Reihen und ein Parallelschwingkreis, bestehend aus jeweils einem Kondensator, einer Spule und einem Widerstand, dar. Sie sind in Abbildung 4 zu sehen. Dabei sind die Energieverluste an Spule und Kondensator im ohmschen Widerstand R zusammengefasst. Die Energieverluste an den Kondensatoren bewegen sich im Vergleich zu Spulen im Bereich von 0,1 bis 1 Promille, weshalb R in Abbildung 4 stets in Reihe mit L geschaltet wird.
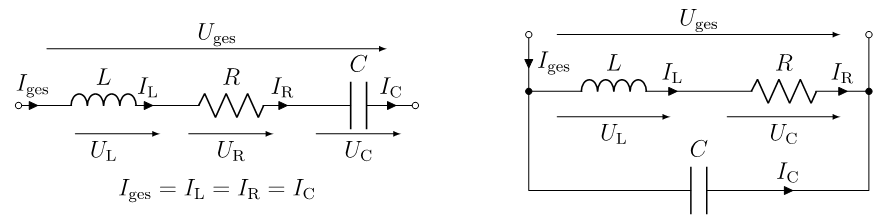
Nachfolgend wird das Verhalten des Parallelschwingkreises (in Abbildung 4 rechts) genauer untersucht. Die komplexe Impedanz Z des Parallelschwingkreises berechnet sich zu
$$ Z(f) = \frac{1}{\frac{1}{R + j 2 \pi f L} + j 2 \pi f C} = \frac{R}{\left(1 – (2 \pi f)^2 C L \right)^2 + (2 \pi C R)^2} + j \frac{2 \pi f (C R^2 – L) – (2 \pi f)^3 C L ^2}{\left(1 – (2 \pi f)^2 C L \right)^2 + (2 \pi f C R)^2} $$
und ist abhängig von der Frequenz f. Wird die Schaltung mit der Resonanzfrequenz (R → 0)
$$ f_R = \frac{1}{2 \pi L} \sqrt{\frac{L}{C} – R^2} \approx \frac{1}{2 \pi \sqrt{L C}} $$
angeregt, dann verschwindet der Imaginärteil der Impedanz und zu den Klemmen hin verhält sich die Schaltung wie eine hochohmige Last. Ist der Serienwiderstand R der Spule sehr klein, kann die Näherung der Resonanzfrequenz für ideale Bauelemente aus obiger Formel verwendet werden. Wird der Betrag der Impedanz des Parallelschwingkreises über die Frequenz f aufgetragen, so erreicht er sein Maximum im Resonanzfall. Dies ist in Abbildung 5 zu sehen.
Der Schwingkreis weist für f ≪ fR ein induktives und für f ≫ fR ein kapazitiv niederohmiges Verhalten auf. Entsprechend weist die Phase der Impedanz einen Nulldurchgang bei der Resonanzfrequenz auf, wie in Abbildung 6 beobachtet werden kann.
Reihen- und Parallelschwingkreise sind duale Schaltungen. Aus diesem Grund kann für den Reihenschwingkreis das entgegengesetzte Verhalten bei der Resonanzfrequenz beobachtet werden. Betrag und Phase des Serienschwingkreises sind in Abbildung 7 und Abbildung 8 dargestellt. Für f ≪ fR weist der Serienschwingkreis ein kapazitives und für f ≫ fR ein induktiv hochohmiges Verhalten auf, während die Impedanz bei der Resonanzfrequenz minimal wird.
Für die Erstellung der obigen Graphen wurden folgende Werte angenommen: L = 100mH, C = 0.92µF und R = 1Ω. Die Werte sind typisch für ein Freileitungskabel mit einer Länge von 100 km. Die Resonanzfrequenz ergibt sich bei ca. 500Hz. Soll die Bandbreite der Resonanz verändert werden, so kann dies beispielsweise über einen höheren Widerstandswert erreicht werden. Dies ist im Gegensatz zu Freileitungskabeln bei Erdkabeln der Fall, die im Mittel- und Niederspannungsnetz vielfach Verwendung finden. Bei einem größeren Widerstand wird die Schwingung stärker abgedämpft und die Resonanz ist weniger stark ausgeprägt. Gleichzeitig werden höhere ohmsche Verluste im Schwingkreis umgesetzt. Für die folgenden Abbildungen 9 und 10 wurde der Widerstand auf R = 100Ω erhöht.
Die Resonanzfrequenz wird im idealen Serienschwingkreis durch eine Veränderung des Widerstandes nicht erhöht. Sie kann über eine Variation der Induktivität oder der Kapazität beeinflusst werden. In Energieübertragungssystemen geschieht dies beispielsweise durch den Einsatz von Doppelleitungen, die die Induktivität verringern.
In realen Energieübertragungssystemen können durch die Verschaltung der Vielzahl von Betriebsmitteln bei beliebigen Frequenzen Resonanzen auftreten. Je nach Betrags- und Phasenverlauf können die Resonanzen in einer Impedanzkurve dann in Parallel- und Reihenresonanzen unterteilt werden.
Wie hängen Impedanz, Resonanzen und Power Quality zusammen?
Das Verbundnetz besteht aus einer Vielzahl zusammengeschalteter Betriebsmittel. Alle diese Betriebsmittel – beispielsweise Leitungen, Transformatoren oder Verbraucher – weisen je nach angeregter Frequenz unterschiedliches Verhalten auf. Anders ausgedrückt: Das elektrische Energienetz ist ein riesiger gekoppelter Schwingkreis aus kapazitiven, induktiven und ohmschen Elementen mit mehreren Resonanzfrequenzen. Wird die Netzimpedanz über einen längeren Zeitraum von einem beliebigen Netzverknüpfungspunkt (NVP) aus gemessen, so wird sie sich stetig ändern, je nachdem, welche Lasten oder Einspeisungen gerade zu- oder abgeschaltet werden. Ein Netzverknüpfungspunkt kann durch ein Thévenin-Ersatzschaltbild, bestehend aus einer idealen Spannungsquelle und einer in Reihe geschalteteten Impedanz, modelliert werden. Für den Nieder- und Mittelspannungsbereich dominieren ohmsche und induktive Komponenten der Netzimpedanz. Aus diesem Grund kann der Netzvernküpfungspunkt wie in Abbildung 11 dargestellt werden.
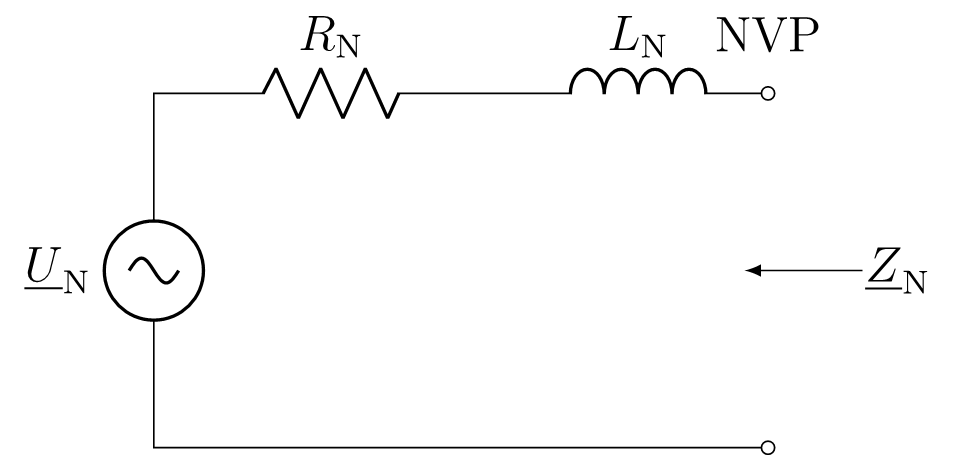
Hierbei bezeichnet \(\underline{U}_N\) die Nennspannung des Netzes. Wird am Netzvernküpfungspunkt ein ohmscher Widerstand mit definiertem Wert angeschlossen, so können Strom und Spannung gemessen und daraus die Netzimpedanz berechnet werden. Die für die Messung der spektralen Netzimpedanz \(\underline{Z}_N\) nötige breitbandige Anregung erfolgt über eine zufällig generierte Pulssequenz, nach der der Widerstand zum Netz hinzugeschaltet wird. Abbildung 12 zeigt beispielhaft die gemessene spektrale Netzimpedanz an einer Steckerleiste mit angeschlossenem Computernetzteil von 0 bis 150kHz. Der Betrag ist in blau dargestellt, während die Phase durch die grüne Kurve repräsentiert wird.
Deutlich erkennbar ist die Parallelresonanz bei ca. 80kHz. Der Betrag der Netzimpedanz ist bei dieser Frequenz maximal während die Phase einen Nulldurchgang hat. In diesem Fall wurde die Resonanz aufgrund des kapazitiven Eingangsfilters des Computernetzteiles hervorgerufen.
Mit der Messung der spektralen Netzimpedanz lassen sich jedoch nicht nur Resonanzen erkennen. Auch Netzrückwirkungen lassen sich anhand von Peaks in der Messkurve identifizieren. Netzrückwirkungen bezeichnen hochfrequente Ströme, die in das Energieversorgungsnetz zurückgespeist werden und damit den Oberschwingungsanteil der Netzspannung und des Stromes erhöhen. Wie im vorigen Abschnitt erklärt wurde, nehmen hochfrequente Ströme überwiegend aufgrund der zunehmenden Zahl leistungselektronisch gekoppelter Erzeuger und Verbraucher zu. Trifft die Frequenz der Oberschwingungsströme auf Reihenresonanzen (niedriger Betrag der Impedanz), so können sehr hohe Ströme ungehindert fließen und damit Betriebsmittel schädigen. Kontinuierliche Power-Quality-Messungen können in Kombination mit Impedanzmessungen zur Resonanzerkennung Schädigungen und Ausfälle durch Oberschwingungsströme detektieren.

